Tiny AES Python
A tiny implementation of AES ECB encryption in Python. Github link of source code.
Recently for an Applied Cryptography class at KTH I had to write from scratch an implementation of the AES encryption. AES is a block cypher encryption that operates on blocks of different sizes. I implement AES-128 in ECB mode which takes 16 byte blocks in a matrix of 4 by 4. What follows is a small implementation in Python with some explanations around each AES step.
Overall structure of AES
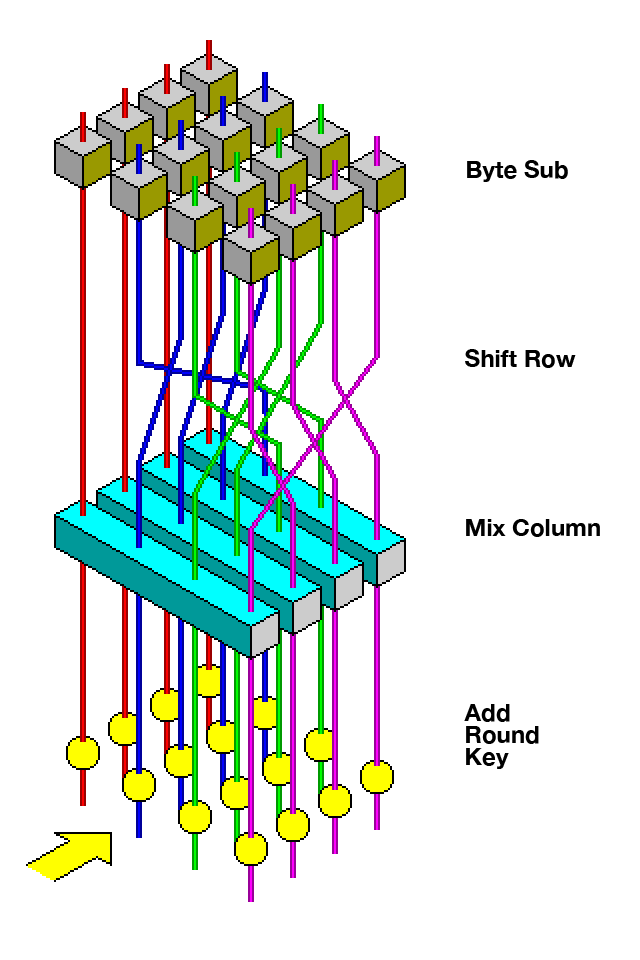
AES is quite a big and detailed process. I won’t go into the details of how each round works as that would require a series of posts instead of one post. Maybe in the future I’ll expand on this. Here is the high-level structure of the algorithm that I got from Wikipedia –
- Key Expansion
- Initial Add Round Key
- 9 rounds of –
- Sub Bytes
- Shift Rows
- Mix Columns
- Add Round Key
- Final round of –
- Sub Bytes
- Shift Rows
- Add Round Key
Implementation
This particular implementation was written to work with Kattis automated testing so it reads stdin as binary data and outputs the encrypted values to stdout in binary data. It probably won’t be a big change to switch this to standard Hex values for better readability but I haven’t gotten around to doing this since the class ended.
Formatting Inputs
The functions below help to convert the 16 byte strings into a list and eventually into a matrix. The transpose function is also needed later in the main encryption function.
def space_input(text):
""" Converts a string into 2 character hex list """
state = []
while text:
state.append(text[:2])
text = text[2:]
return state
def bytes_2_matrix(text):
""" Converts a 16-byte array into a 4x4 nested list matrix """
state = [list(text[i:i+4]) for i in range(0, len(text), 4)]
state = transpose_matrix(state)
return state
def transpose_matrix(state):
""" bytes 2 matrix result needs to be transposed for correct order """
temp = []
for j in range(NUM_BLOCKS):
row = []
for i in range(NUM_BLOCKS):
val = state[i][j]
if len(val) == 3:
state[i][j] = '0x0' + val[2]
row.append(state[i][j])
temp.append(row)
return temp
Initial Key Expansion
For key expansion, we take the 16 byte key that we have and expand it to 176 bytes. Each of these is then passed into each round of AES as a round key.
def rotate_bytes(bytes):
temp = bytes[0]
bytes[0] = bytes[1]
bytes[1] = bytes[2]
bytes[2] = bytes[3]
bytes[3] = temp
return bytes
def sbox_lookup(bytes):
for i in range(NUM_BLOCKS):
srow = int(bytes[i],16) // 16
scol = int(bytes[i],16) % 16
hex_sbox = SBOX[srow][scol]
bytes[i] = hex(hex_sbox)
return bytes
def expand_key(master_key, expanded_key):
rcon = 1
last_four_col = [0 for x in range(NUM_BLOCKS)]
for i in range(0, len(master_key), 1):
expanded_key[i] = hex(int(str(master_key[i]),16))
done_with = 16 # counter for how many bytes we're done expanding
total_expanded_bytes = 176
while done_with < total_expanded_bytes:
for i in range(NUM_BLOCKS):
last_four_col[i] = expanded_key[i + done_with - 4]
if (done_with % 16 == 0):
last_four_col = rotate_bytes(last_four_col)
last_four_col = sbox_lookup(last_four_col)
last_four_col[0] = hex(int(last_four_col[0],16) ^ RCON_TABLE[rcon])
rcon = rcon + 1
for i in range(NUM_BLOCKS):
expanded_key[done_with] = hex(int(str(expanded_key[done_with - 16]),16) ^ int(str(last_four_col[i]),16))
done_with = done_with + 1
return expanded_key
Add Round Key
Here we just xor the byte of the state with the byte of the key. State here refers to our 4×4 matrix that we are trying to encrypt.
def add_round_key(state, key):
key_matrix = bytes_2_matrix(key) # convert list into matrix for easier xor order
for row in range(NUM_BLOCKS):
for col in range(NUM_BLOCKS):
state[row][col] = hex(int(str(state[row][col]), 16) ^ int(str(key_matrix[row][col]), 16))
return state
Sub Bytes
Replace each byte of the state with the corresponding in the lookup table (SBOX).
def sub_bytes(state):
for i in range(NUM_BLOCKS):
for j in range(NUM_BLOCKS):
val = int(state[i][j], 16)
state[i][j] = hex(SBOX[val//16][val%16])
return state
Shift Rows
The first row is left as is. The second row is shifted left twice. The third row is shifted left thrice. The last row is shifted left three times.
def shift_rows(state, row, num_shifts):
for _ in range(num_shifts):
temp = state[row][0]
for j in range(3):
state[row][j] = state[row][j+1]
state[row][3] = temp
return state
def shift_rows_wrapper(state):
for i in range(1, 4):
state = shift_rows(state, i, i)
return state
Mix Columns
Taking the last column at a time and using matrix multiplication on it with an xor function. This is explained better in many other places, including here.
def mix_columns(state):
mixed_state = [
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]
]
col_pick = [x for x in range(NUM_BLOCKS)]
mix_col_val = [x for x in range(NUM_BLOCKS)]
for col in range(NUM_BLOCKS):
for row in range(NUM_BLOCKS):
col_pick[row] = int(state[row][col], 16)
mix_col_val[0] = MULTIPLY2[col_pick[0]//16][col_pick[0]%16] ^ MULTIPLY3[col_pick[1]//16][col_pick[1]%16] ^ col_pick[2] ^ col_pick[3]
mix_col_val[1] = col_pick[0] ^ MULTIPLY2[col_pick[1]//16][col_pick[1]%16] ^ MULTIPLY3[col_pick[2]//16][col_pick[2]%16] ^ col_pick[3]
mix_col_val[2] = col_pick[0] ^ col_pick[1] ^ MULTIPLY2[col_pick[2]//16][col_pick[2]%16] ^ MULTIPLY3[col_pick[3]//16][col_pick[3]%16]
mix_col_val[3] = MULTIPLY3[col_pick[0]//16][col_pick[0]%16] ^ col_pick[1] ^ col_pick[2] ^ MULTIPLY2[col_pick[3]//16][col_pick[3]%16]
for index in range(NUM_BLOCKS):
mixed_state[index][col] = hex(mix_col_val[index])
return mixed_state
Encryption
The code above is all the functions we need. The functions just repeat over each round with new round keys from our key expansaion. We bring it all together in our main encryption function below.
def encrypt(message, keyinput):
key = keyinput
message = space_input(data)
state_matrix = bytes_2_matrix(message)
EXPANDED_KEY = [0 for x in range(176)]
expanded_key = expand_key(key, EXPANDED_KEY)
round_key = [0 for x in range(len(expanded_key)//16)]
for i in range(len(round_key)):
round_key[i] = expanded_key[i*16:i*16+16]
state_matrix = add_round_key(state_matrix, round_key[0])
for i in range(1, NUM_ROUNDS):
state_matrix = sub_bytes(state_matrix)
state_matrix = shift_rows_wrapper(state_matrix)
state_matrix = mix_columns(state_matrix)
state_matrix = add_round_key(state_matrix, round_key[i])
state_matrix = sub_bytes(state_matrix)
state_matrix = shift_rows_wrapper(state_matrix)
state_matrix = add_round_key(state_matrix, round_key[10])
#check the encryption string
state_matrix = transpose_matrix(state_matrix)
cipher_list = [i for sub in state_matrix for i in sub] # flatten nested list into 1D list
cipher = "".join(cipher_list).replace('0x','')
return cipher
Main Function
The main function where we obtain the stdin and send the stdout as well as break down the input by 16 bytes at a time for better performance.
if __name__ == '__main__':
#For Kattis
key = sys.stdin.buffer.read(16).hex()
key = space_input(key)
while True:
data = sys.stdin.buffer.read(16).hex()
if not data:
break
ciphered = encrypt(data, key)
sys.stdout.buffer.write(bytes.fromhex(ciphered))
Summary
AES is not an easy concept to grasp. It took me a while to understand all the functions and how they relate together. Once I got the overall understanding from referencing many resources and external help the implementation became quite straightforward. This was quite a fun program to write afterwards. The whole code can be found on my Github link below. Due to limitations with Python and Kattis timeouts the program only passes 9/10 Kattis test cases as it runs into memory/timeout limits on Kattis for the last test. It would be fun to implement this in a more low-level programming language like Rust.
Source code – Tiny AES
